Ich hatte diese Kritik im Rahmen des (wahnsinnig tollen) Daten-Labors 2015 nebenbei geäußert und dann aufgrund des Interesses versprochen meine Gedanken aufzuschreiben. Hier sind sie nun endlich.
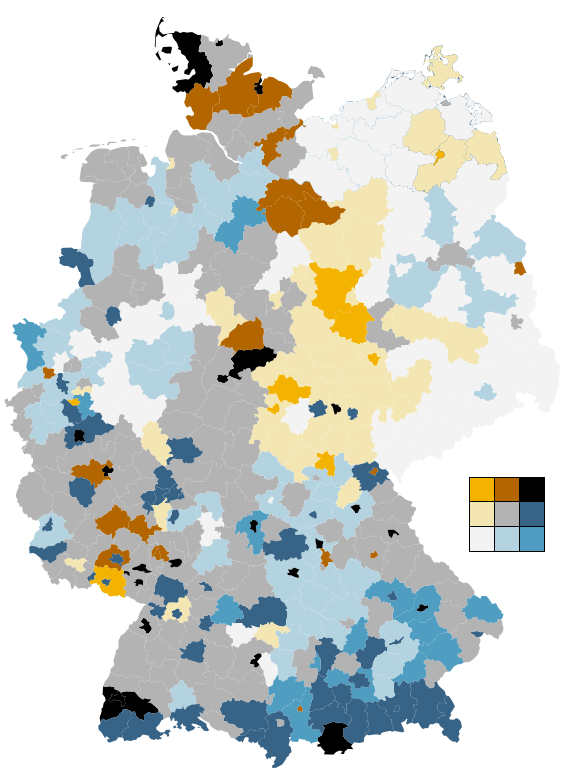
Geld zieht Ärzte an, so titelte die Zeit Online vor einigen Monaten über einer Recherche zum Verhältnis der räumlichen Verteilung von Ärzten im Vergleich mit verschiedenen demographischen Faktoren. Integraler Bestandteil des Artikels sind komplexe Karten und Diagramme. Die Redakteure versuchten sich an der Verwendung einer bivariaten Klassen-/Farb-Skala, doch leider ging die Wahl der Farben daneben, so dass das Endprodukt ineffektiv und irreführend ist. Es geht mir hier ausschließlich um die kartografische Darstellung. Zum Inhalt und der Datenanalyse kann ich nichts sagen!
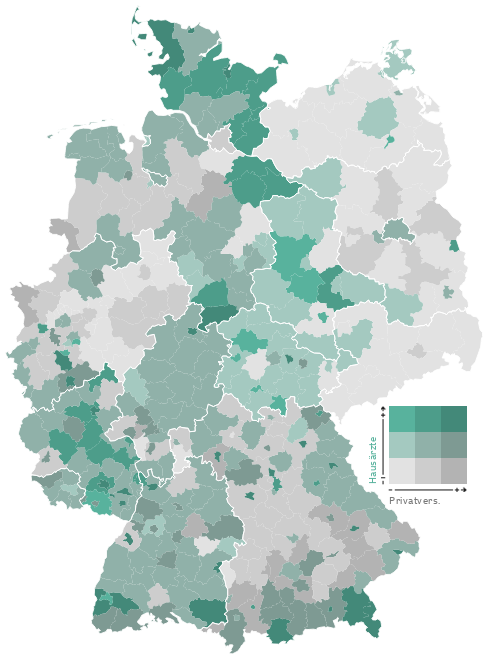
So funktionieren die Karten: Grau steht für Privatpatienten, Grün für Ärzte. Zu den drei Helligkeitsstufen (je dunkler, desto höher der Anteil der Privatversicherten) kommt die Farbe dazu (je intensiver, desto mehr Ärzte pro Einwohner) So ergeben sich neun verschiedene Werte für die Einfärbung der Karten.
Quelle: http://www.zeit.de/feature/gesundheit-arzt-privat-versicherung-praxis
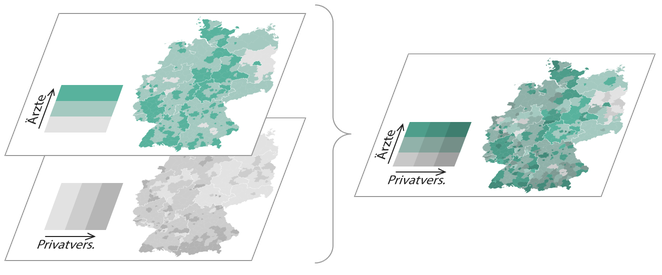
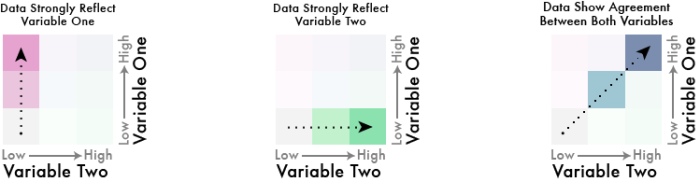
In einer bivariaten Skala wird das Verhältnis zweier Variablen zueinander/miteinander in vollem Detail dargestellt. Anstelle einer einzelnen Verhältniszahl sind hier mehrere Achsen im Gebrauch und damit die einzelnen Werte der Variablen nachvollziehbar. Solche Skalen sind in der Kartographie an sich nichts neues, werden allerdings (aufgrund der Komplexität meiner Meinung nach zu Recht) eher selten verwendet. Im Frühjahr 2015 veröffentlichte Joshua Stevens einen fantastischen Artikel, dessen Lektüre ich vor dem Weiterlesen sehr empfehle.
Joshua zeigt dort, wie aus den jeweiligen Farbskalen der beiden Attribute eine gemischte “Matrix” entsteht. Die Diagonale wird hierbei zu einem neuen sequenziellen Farbverlauf, der das neutrale Verhältnis der Variablen anzeigt. Die Farbskalen müssen dementsprechend mit Bedacht gewählt werden, so dass sich bei ihrer Vermischung eine sinnvolle, geordnete und “eigenständige” Skala entsteht.
Quelle: http://www.joshuastevens.net/cartography/make-a-bivariate-choropleth-map/
In Joshuas Beispiel sind (relativ) klar differenzierbar und identifizierbare Achsen entstanden, die dem Kartenbetrachter (mit etwas Anstrengung) ermöglichen, die Karte korrekt zu interpretieren. Man kann anhand der Farbe das jeweilige Verhältnis und die absoluten Werte lesen. Die Farbachsen sind intuitiv korrekt sortierbar.
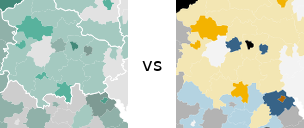
Wie sieht es mit dem Farbschema der Zeit aus? Leider nicht gut.
Die Redakteure wählten für die eine Variable einen Farbverlauf von Grau nach Grün, für die andere einen von Grau nach Dunkelgrau (siehe oben). Die diagonale Farbskala entsteht also aus der Vermischung von Grün und Grau. Was passiert, wenn man Grün und Grau mischt? Man bekommt Farbtönen zwischen Grün und Grau… Die Farben auf der Diagonalen werden also sehr ähnlich zu zumindest einer der Hauptachsen. Damit zeigen sich Farben im Kartenbild, deren Ordnung der Betrachter unmöglich intuitiv und auch mithilfe der Legende kaum mental durchführen kann. Und genau das können wir hier sehen:
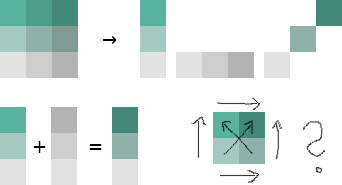
Als kleine Demonstration wieviele Details und Strukturen tatsächlich in den Daten stecken, habe ich einfach mal eine bivariate Farbskala von Cynthia Brewer auf die Daten geworfen. Achtung: Ich habe die Klassen nicht genau so legen können (Faulheit), wie sie in der Ursprungskarte vorliegen! Grundsätzlich dürfte die Aussage der Karte aber stimmen. Die Ästhetik steht erstmal an zweiter Stelle. ;)